The AEE is a subsystem that slots into any RPG for simulating everything from Bad Weather to Plagues & Poisons.

The Backstory

A while back, I was working on an adventure for one my campaigns (being deliberately vague, here) and I needed to look up the effects of Cobra Venom in the Hero System.

I wasn’t impressed – this stuff is supposed to be dangerous, even deadly, and what was offered in the bestiary supplement would barely kill a child.

And this particular venom was supposed to derive from supernatural Cobras summoned by a pissed-off deity. So that wouldn’t cut it.

I developed the Venom described in the box below, but wasn’t very happy with it – too fiddly, and perhaps a touch TOO lethal.
 
 
 
 
 

PER HIT:

• Immediate on exposure: -5 all primary stats -2 PD -2 ED -10 END -1 ALL SKILLS -2 OCV -2 DCV plus 10 STUN 1 BODY dmg
• Round after exposure: -3 all primary stats -1 PD -1 ED -6 END -1 ALL SKILLS -1 OCV -1 DCV (all cumulative) plus 10 STUN 2 BODY dmg
• 2nd round after exposure: -2 all primary stats -4 END -1 ALL SKILLS -1 OCV -1 DCV (all cumulative) plus 5 STUN 3 BODY dmg
• 3rd, 4th, rounds after exposure: -1 all primary stats -2 END plus 3 STUN 2 BODY
• 5th round after exposure: -1 all primary stats -1 PD -1 ED -2 END -1 ALL SKILLS -1 OCV -1 DCV plus 2 STUN 1 BODY
• 6th, 7th round after exposure: as per 3rd & 4th rounds
• 8th round after exposure: as 5th round
• 9th, 10th round after exposure: -2 END plus 2 STUN 1 BODY

These are accompanied by appropriate physical & mental responses – shaking, stumbling, delirium, semi-consciousness, poor decision-making, extreme pain (burning sensations) etc. The wound site will blister as though exposed to Mustard Gas or a gas stove’s flame, and the effect will slowly spread through the 10 rounds, starting 2-3 cm diameter +1 cm diam each subsequent round..

TOTAL EFFECTS:

-5-3-2-2-1-2-1= -16 all primary stats;
-2-1-1-1 = -5 PD same ED;
-10-6-4-2-2-2-2-2-2-2 = -32 END;
-1-1-1-1-1=-5 ALL SKILLS;
-2-1-1-1-1=-6 OCV & DCV;
10+10+5+3+3+2+3+3+2+2 = 43 STUN
1+2+3+2+2+1+2+2+1+1 = 17 BODY

Clothing: Adds 1 round delay to the above

A tornique: Halves the rate of effect shown

Antivenom: Stops effects instantly, restores 1/4 of the damage taken to stats & skills (round down)

If the character survives the course of the attack and does not get hit again, he can recover:

1 Primary stat point (each stat) / 30 mins
1 OCV & DCV / 30 mins
1 Secondary stat point / hour
END as Normal
STUN as 1/2 Normal
BODY as Normal

Those second thoughts didn’t happen right away – in fact, there was about a year in between generating and reviewing the above, and we’re still nowhere near it appearing in play, which it may never do, so I marked it for reconsideration and moved on to higher-priority tasks.

Then, a few weeks ago, in Traits of Exotic d20 Substitutes pt 1, I casually tossed out a completely original system (inspired by the Sixes System, for which I still have to write the final part).

A number of people seemed to like its elegance and simplicity and flexibility. So, a couple of days later, when I came across my note to review the Cobra Venom, the two thoughts clicked together.

But, to actually be usable in play, I needed to dig deeper into what was a casual aside at the time. And so, here we are.

The Core System

The GM specifies N dice, and a target of T sixes. At intervals (generally fixed by the GM but may be variable), the character rolls Nd6. Any sixes are counted towards T, until the total is T or more.

If one 1 is showing, something bad happens (specified by the GM but not necessarily announced).

If two 1s are showing, something worse happens (specified as above). Or the same bad thing happens twice. Or the same bad thing happens, and some other bad thing happens. Whatever – it’s worse.

If three 1s are showing, something really bad happens (specified as above). And T might increase by 1. Or one of the alternatives listed previously. It’s useful to be consistent.

If four or more 1s are showing, something catastrophically bad happens and T increases by 1 or more. Or (you guessed it) as above.

You also have the option of specifying a very small ‘something bad’ if no 1s are showing, just to remind the victim that they have this hanging over their head.

The GM controls the severity of each level of effect, the frequency of rolls, the size of the rolls (N), and the target (T). The combination of N and T also dictates what the frequency of occurrence of the different levels of penalty should be.

Nice, neat, and simple – in theory.

To really use it in practice, the GM needs a way to estimate what the total effects are likely to be. Then he can adjust the penalty levels and N and T accordingly to get exactly what he wants the probable outcome to be.

Or he can start with predetermined outcomes in mind and divide them up into the different penalty levels according to a convenient pairing of N and T, based on E, the number of rolls it’s expected to take to reach T.

On Today’s Menu

I’m going to outline the process in full, with tables and convenient shortcuts built in for the GM, for the first approach. Then I’ll outline the second in a shorter format, because it will use the same tables as the first approach.

When I was planning and contemplating this expansion, I also thought up a number of variations, so I’ll describe them and their impacts as the cherry on top.

Set N and T

These should always be determined by E, the expected number of rolls to reach T rolling N dice at a time.

T=1, for N=1 to 8: 6, 3, 2, 2, 2, 1, 1, 1
T=2, for N=1 to 8: 12, 6, 4, 3, 3, 2, 2, 2
T=3, for N=1 to 8: 18, 9, 6, 5, 4, 3, 3, 3
T=4, for N=1 to 8: 24, 12, 8, 6, 5, 4, 4, 3
T=5, for N=1 to 8: 30, 15, 10, 8, 6, 5, 5, 4
T=6, for N=1 to 8: 36, 18, 12, 9, 8, 6, 6, 5
T=7, for N=1 to 8: 42, 21, 14, 11, 9, 7, 6, 6
T=8, for N=1 to 8: 48, 24, 16, 12, 10, 8, 7, 6

or, you might prefer to pick an N and then a T:

N=1, T=1 to 8: 6, 12, 18, 24, 30, 36, 42, 48
N=2, T=1 to 8: 3, 6, 9, 12, 15, 18, 21, 24
N=3, T=1 to 8: 2, 4, 6, 8, 10, 12, 14, 16
N=4, T=1 to 8: 2, 3, 5, 6, 8, 9, 11, 12
N=5, T=1 to 8: 2, 3, 4, 5, 6, 8, 9, 10
N=6, T=1 to 8: 1, 2, 3, 4, 5, 6, 7, 8
N=7, T=1 to 8: 1, 2, 3, 4, 5, 6, 6, 7
N=8, T=1 to 8: 1, 2, 3, 3, 4, 5, 6, 6

Don’t worry about these not lining up in neat columns, the same information is available in the table that is below.

Advice:

I prefer this approach because of the clear patterns shown for N=1, 2, 3, and 6 – but these can be misleading if used for extrapolation, as N=4 shows with its jump from 3 to 5, and N=5 shows with the jump from 6 to 8, with the second of these being the stronger example. So the extrapolation is not as certain as a pattern might suggest, and can’t be relied on – so I will always recommend using the first arrangement, simply because it doesn’t suggest potentially misleading extrapolations.

High-T = long durations, especially with lower N values. That’s suitable for diseases that have a long interval between checks – every 12 or 24 hours, say. But for poisons, you don’t want an E that’s more than 6 or 8, even for the worst ones, and 5-6 is probably a better target even for those. E=3-4 is good for mid-strength poisons, and E=1-2 should really be reserved for only the fastest-acting.

For every really lethal poison or disease, there should be several of the mid-strength variety, and for every mid-strength, many weaker poisons – or so runs one line of thinking. But evolution favors those poisons that are strong enough to take down whatever the poisoner feeds on or is commonly attacked by; it doesn’t happen in isolation. That can cause potency to increase, moderating the earlier trend. So here are a trio of ratios to get you thinking:

By Theoretical Threat Magnitude: 1: 3: 9-12
By Evolutionary End-point: 1 : 2 : 3
Compromise: 2 : 5 : 10

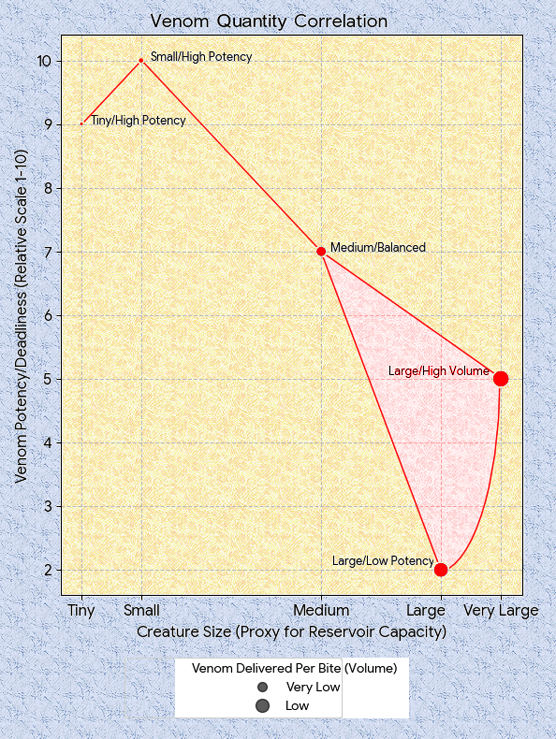
Playing into that decision should be the poison reservoir. In other words, how many bites of the poison cherry can one poisoner deliver?

Size of the creature impacts this – the larger the creature, the larger the venom sacs (or their equivalent).

Here are some real-world assessments:

Tiny/Small – insects, small spiders, scorpions, small centipedes – venom capacity is very low and either single-use or low-frequency bursts. The venom is metabolically costly relative to body size. Often have a single, full dose for immediate defense/predation. Recovery is long (hours/days).

Medium – mid-sized snakes, large spiders, cone snails, large scorpions, etc – Moderate venom capacity, low-moderate frequency of delivery – three uses in quick succession. Capable of venom metering – injecting less than maximum to conserve supply. May deliver a full dose for a large threat, or a “dry bite” (no venom). Can deliver a burst of 2-3 significant bites, then need short recovery (minutes).

Large – large snakes, octopuses, large fishes – high venom reservoirs, Moderate-high frequency of use (multiple uses or sustained delivery). High reservoir allows for multiple, significant envenomations. Gaboon Vipers, in particular, are known for a massive venom yield and ability to deliver repeated, high-volume strikes. Delivery can be sustained over a short period. Recovery time for full capacity is still long, but practical use is frequent.

As a general rule of thumb, the less venom, the deadlier it has to be, because volume decreases as the cube of linear size. The venom therefore has to become more potent just to keep up. Larger creatures have much more venom, which they can utilize in a number of different ways, one species compared to another. On top of that, smaller creatures are less physically resilient, and need to end combat encounters more quickly in order to survive – so that’s an extra push toward higher toxicity

The graphic below was provideded by Gemini, Google’s AI, and edited by me:

I also asked Gemini to extrapolate its’ findings to cover giant and ‘dire-” creatures, and this is what it came back with (edited):

Gargantuan Creatures – 5m long spiders, Giant Snakes: Size factor 5-10 x earth “real”. Venom Capacity up to 50x that of normal equivalents. Potency may decrease slightly, but total damage output increases exponentially due to volume. Sustained High Frequency of venom delivery, can deliver (5-10x earth “real”) lethal doses with minimal pause. (May take weeks to recharge but still have sufficient venom for 2-3 encounters while recharging).

Colossal Creatures – 25m sea creatures, “Kaiju” spiders, etc. Size Factor 25+ times earth “real”. Venom Capacity – essentially unlimited. Potency is often low relative to size, but the volume is so immense it acts as a biological (or breath weapon, acid spray, etc, with toxic effects on top). The creature’s bite/sting is less about injecting a dose and more about dousing the target (and/or the environment around it).

A “Dire Version” is a creature that defies the standard biological trade-off, making it inherently more dangerous and a true “boss” encounter. The Dire modifier should break the Inverse Correlation by increasing both Reservoir Size and Venom Potency.

So, once you have T, N and E, and have started thinking about bite frequency vs toxicity

Probable Occurrence of Adverse Effects

By the way, before it begins – generating this table of results proved too complicated for both Gemini and ChatGPT! Both understood clearly what I wanted them to do, and (as much as an LLM can) why, and generated a solution to the problem of how – that didn’t work.

Repeated corrections were attempted in both cases, and failed. That’s not a measure of my intellect or anything like that – it’s an indication of just how much detailed work lies under the surface of this innocuous-looking table.

If I had a BASIC compiler, I could have written the code myself from one of their algorithms in less time, and in about 20 lines.

Key:

“No +” represents low chance of more. Use the indicated number of occurrences in estimating total impact from impact per occurrence.

“+” represents a moderate chance of more. Use the indicated number of occurrences in estimating total impact from impact per occurrence.

“++” represents a significant chance of more. Use the indicated number of occurrences + 0.5 to estimate the average total impact from impact per occurrence.

“+++” represents a high likelihood of more occurrences than the number shown, and a high confidence of at least this many occurrences. Use the indicated number +1 to estimate the average total impact from impact per occurrence.

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
T	N	E	K=1	K=2	K=3	K=4	K=5	K=6	K=7	K=8
1	1	6	1
1	2	4	1	0
1	3	3	1	0	0
1	4	2	0+++	0	0	0
1	5	2	0+++	0+	0	0	0
1	6	1	0+++	0+	0	0	0	0
1	7	2	0+++	0+	0	0	0	0	0
1	8	1	0++	0++	0	0	0	0	0	0

 

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
2	1	12	2
2	2	7	1+++	0
2	3	5	1++	0+	0
2	4	4	1++	0+	0	0
2	5	3	1	0+	0	0	0
2	6	3	1	0+	0	0	0	0
2	7	3	1	0++	0	0	0	0	0
2	8	2	0++	0++	0	0	0	0	0	0

 

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
3	1	18	3
3	2	10	2+++	0+
3	3	7	2+	0+	0
3	4	5	1+++	0++	0	0
3	5	4	1++	0++	0	0	0
3	6	4	1++	0+++	0	0	0	0
3	7	3	1	0++	0	0	0	0	0
3	8	3	1	0+++	0+	0	0	0	0	0

 

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
4	1	24	4
4	2	13	3++	0+
4	3	9	3	0++	0
4	4	7	2++	0+++	0	0
4	5	5	2+	0+++	0	0	0
4	6	5	2	1	0+	0	0	0
4	7	4	1++	0+++	0+	0	0	0	0
4	8	4	1++	0+++	0+	0	0	0	0	0

 

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
5	1	30	5
5	2	16	4+	0+
5	3	11	3+++	0+++	0
5	4	8	3	0+++	0	0
5	5	7	2+++	1	0	0	0
5	6	6	2+	1	0+	0	0	0
5	7	5	1+++	1	0+	0	0	0	0
5	8	5	1+++	1+	0++	0	0	0	0	0

 

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
6	1	36	6
6	2	19	5+	0++
6	3	13	4++	0+++	0
6	4	10	3+++	1	0	0
6	5	8	3	1+	0+	0	0
6	6	7	2+++	1+	0+	0	0	0
6	7	6	2+	1+	0+	0	0	0	0
6	8	5	1+++	1+	0++	0	0	0	0	0

 

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
7	1	42	7
7	2	22	6	0++
7	3	15	5	1	0
7	4	11	4	1+	0	0
7	5	9	3++	1+	0+	0	0
7	6	8	3	1++	0+	0	0	0
7	7	7	2++	1++	0++	0	0	0	0
7	8	6	2	1++	0++	0	0	0	0	0

 

T = target number of 6s
N = number of dice at a time
E = expected number of rolls required, on average
K = number of cases of k ones showing over the span of E rolls
8	1	48	8
8	2	25	6+++	0++
8	3	17	5+++	1	0
8	4	13	5	1++	0	0
8	5	10	4	1++	0+	0	0
8	6	9	3++	1+++	0+	0	0	0
8	7	8	3	1+++	0++	0	0	0	0
8	8	7	2++	1+++	0++	0	0	0	0	0

E is usually a decimalized number because the calculations determine the average outcome over many sets of rolls. “2.6” means that 40% of the time it will take 2 rolls and 60% of the time it will take 3 – but there is always an outside chance that it might take 1 or 4, so those percentages are approximate. Because in the real world you can’t have “0.6 of a roll”, these have been rounded up, and the resulting whole number of rolls used to calculate the rest of the table.

If you want to know the exact query that ‘broke’ the AIs, it was something like this:

For N 6-sided fair dice from 1 to 8, calculate the number of rolls required to reach a total number of sixes shown across all rolls equal to or greater than T, which also varies from 1 to 8, and label it E1. Because in the real world you can’t have “0.6” of a roll, round E1 up and label it E. For E rolls of N fair six-sided dice, calculate the number of rolls exactly K 1s will be seen, with K varying from one to 8. If the result for a given K (designated R) is an integer, show the integer; else if RK-INT(RK) is <0.25, show INT(RK); else if RK-INT(RK) is <0.5, show INT(RK) and one “+” sign; else if RK-INT(RK) is <0.75, show INT(RK) and two “+” signs; else show INT(RK) and three “+” signs, for example “2+++”. If an entry is impossible, eg K>N, show a blank space, not a 0. Format the results in a plaintext tab-delimited table with columns T, N, E, K=1, K=2, etc, sorted by T and sub-sorted by N.

Note that I had to run this query about 25 times, refining it each time, and eventually had to take out everything relating to the encoding and requesting the answer to 3 decimal places so that I could ‘manually’ do the coding.

Gemini calculated the results correctly, including the formatting, but couldn’t get the columns of data to line up correctly after 24 rows plus the heading – the K=1 column kept overwriting the E column, no matter what was done.

ChatGPT failed completely to apply the encoding correctly and had several calculation errors at first, but with a bit of patience and simplifying the question, did manage to produce a table that I could copy and paste into a spreadsheet. I then inserted additional columns to perform the calculation of RK-INT(RK) and interpret the results as per the “if” statement shown above. I then hid the working and manually transcribed the results into the tables above.

Oh, and for clarity, I decided at the last minute to break what was one big table into the more user-friendly 8 smaller tables.

So let’s pick an entry, I’ll decode it, and show you how it works. How about… 5 dice, target of four 6’s.

1. Look for the line that starts 4 – 5.
2. E is 6, so you can expect the victim to roll 6 times on average before getting to the target of 4 sixes – of course, it could happen on the very first roll, but it probably won’t.
3. So, what’s likely to happen, bad-things wise, over the course of those expected 6 rolls?
   • K=1 has a value of 2+, so there will probably be two times that a single 1 one is showing.
   • K=2 has a value of 0+++ – so the expectation is that this won’t happen on any of them, but there’s a very high chance of it happening at least once – just not a relative certainty of it. And that makes sense – there’s a 1 in 36 that you’ll get 2 ones on two dice, and 25/36 chance that there will be no 1s on the other 2 dice, for a total chance of 25/1296 of this outcome, or 1.9%. But that doesn’t allow for a 1 on the first dice and another 1 on, say, the 3rd dice – so there are more ways for this to happen. And that puts the chance up so high that it’s very likely to happen.
   • K=3 through K=5 are extremely unlikely to occur. Not impossible, but not likely. For all practical purposes, this is a two- or three-tiered penalty structure.
4. The key takeaway, though, is: 2 x one 1, 1 x two 1’s, and 8-3=5 x no 1’s.
5. So multiply that by the chosen harm levels that go with those one-counts, add it up, and you have your expected damage.
   • To demonstrate this, let’s say no 1’s = 1 HP, one 1 = 5 HP, and two 1’s = 10HP. Then we would have 1×5 + 1×10 + 5×1 = 20 HP damage.
6. But the system can be as complicated as you want.
   • Try no 1’s = 2 HP, 1 one = +5 HP, and 2 ones = +10 HP and a point of STR, each accompanied by the lesser levels.
   • Then, we would expect 2x(5+2) + 1x(10+5+2, & 1 STR) + 5×2 = 14+17+10 HP & 1 STR = 41 HP & 1 STR.

Choosing N and T

Unless you are modeling a specific set of conditions that dictate otherwise, or are working to deliver an ‘average fixed amount of damage’ (both covered in subsequent sections), the place to start is with the time intervals* between rolls and the number of rolls expected to be needed, E.

That will give you a short-list (perhaps VERY short) to choose between.

For example, if I want an effect to apply for an average of 6 time-intervals – it could be six rounds, six lots of 30 seconds, 6 minutes, 6 hours, 6 days, or whatever – I would look for E of 5, 6, or 7.

A whopping 17 entries in the table match, so I’m not spoiled for choice. Since there are so many, I would lose the 5’s and 7’s and go with just the options that give exactly what I want.

That gets me down to 5 choices. I want the players to roll more than 1 die but no more than 4, because anything else takes longer to add up.

But that kills all my choices, so the decision is now which restriction do I desire more – the 6 rounds, or the 4 dice?

I decide that 7 rounds is acceptable, after all. That puts a lot of options back on my radar, including T=4 N=4 and T=4, N=5. The first has a higher chance of K=1 results, the latter introduces an outside chance of K=5 and an increased chance of K=3 and K=4. But it does fit my original 6-round desire. In the end, I choose to flip my compromise and choose the N=T=4 option.

Job Done.

Extending The table

Let’s compare the 4-4 line with the 8-8 line.

4-4: 7, 2+, 0+++, 0, 0; vs
8-8: 7, 2++, 1+++, 0++, 0, 0, 0, 0, 0

So you can’t break an 8-8 into two sets of 4-4 rolls. But there is a simple way.

Let’s look at N=12 T=12.

Step 1: Divide both N and T by 2 (they have to be even).

Step 2: Look up the results on the tables above. In this case, we get N=6, T=6.

Step 3: The total number of rolls expected is the same for both – in this case, 7.

Step 4: Because the scaling also increases the deliberately-induced ’rounding error’, subtract 1/2 from the expected number of rolls in response to the doubling. So that’s 6½.

Step 5: The total number of rolls is the same, but doubling the dice makes it easier to roll high numbers of ones. The counts for the worse penalties will increase, while the count for the standard penalty remains stable or slightly decreases. Balanced against that is the fact that the probability of those higher penalties is so low that your increasing nothing by a smidgen in most cases. Analysis has led to the rules for doubling:

• # and #+ are always treated as #.
• ++ should be read as #+1.
• If the full E is <16, +++ should also be read as #+1.
• If E >15, +++ should be read as #+2.

So, in this case, we have 2+++, 1+, 0+, 0, 0, 0.
E is <16, so 2+++ becomes 3.
1+ stays 1.
0+ stays 0.
0 stays 0.

So three single 1s, 1 pair of 1s, and 2.5 rolls without ones.

Step 6: But then we have to factor in the drop from 7 to 6½ expected rolls:

3 x 6.5 / 7 = 2.8 single 1s, 0.93 pairs of 1s, and 6.5 – 2.8 – 0.93 = 2.77 rolls with no 1s.

Step 7: Multiply those by your chosen penalty values.

Let’s use…

No 1’s = 3 HP
One 1 = 10 HP
Two 1s = 25 HP

3 x 2.77 + 10 x 2.8 + 25 x 0.93
= 8.31 + 28 + 23.25 = 59.56 HP.

Step 8: Round up and add the lower of the half N or T to allow for the possibility of those results of 3 or more 1s.

In this case, both are 6, giving a final estimate of 66 HP damage.

It is recommended that + and +++ rolls should have their expected penalties softened, especially if using compound effects, as the levels set for them are based on occurrence numbers that are only partially expected to occur. 10% weaker is about right. Similarly, ++ rolls should be subjected to a moderate reduction (~20%) for the same reason.

Setting penalty levels

Ensure the penalty definitions are geometrically worse as K increases (eg., K=2 is far worse than K=1) to reflect the exponentially decreasing probability of high K rolls.

Setting penalty levels from a designated target

If plugging values into the calculations above doesn’t suit, you can establish a fixed geometric ratio – 2.5, 3, or 4 all work well – and use them to reduce your high K results to a specific number of K=1 or K=0 results. I recommend the first of these, but it’s up to you.

For example, let’s use 6 dice and a Target of 3 sixes. E=4.

One 1 = 1++, treated as 1.5
Two 1s = 0+++, treated as 1.
Three to Six 1s = 0. Ignored.
No 1’s = 4-1-1.5 = 1.5.

And let’s set a nice robust target like 100 HP. That’ll get a PC’s attention in a hurry!

Set the ratio as 4, and let’s extend the calculation down to K=0.

Two ones = 4 (the ratio) single ones, for a total of 5.5 of them.
One one = 4 (the ratio).’no ones’, so 5.5 x 4 = 22.

100/22 = 4.54. Round down to 4. That 4 x 1.5 expected = 6 points, so our target is now 94 points from 5.5 k=1s.

94 / 5.5 = 17.09. Round it down to 17. Multiply by the 1.5 times it’s expected to occur and we get 25.5. So our target goes down by 25 (round it down again) and our K=1 value is 17 HP.

96-25 = 71. So our K=2 – expected once – is 71 HP.

Final results:

K=0 does 4 HP.
K=1 does 17 HP.
K=2 does 71 HP.

Of course, if you set more modest targets, you’ll get more moderate results. This was deliberately extreme.

Variation One: Nested Damage Types

Try this on for size:

K=0: minor HP damage.
K=1: significant HP damage.
K=2: significant HP damage & single-stat damage.
K=3: significant HP damage & second-stat damage.
K=4: Significant HP damage & both stats damaged.
K=5: K=4 + Significant HP damage.
K=6: K=4 + K=2.
K=7: K=4 + K=3.
K=8: 3 x K=4.

These results ‘nest’ three types of damage – two to stats and HP. You can use a similar system if the game system has multiple damage types, as in the Hero System:

K=0: Some END loss
K=1: K=0 + Some Stun loss
K=2: 2 x K=1 + Some Body damage
K=3: K=1 + K=2 + Some temporary Stat loss
K=4: 2 x K=2 + Some temporary Stat loss
K=5: K=4 + K=2
K=6: K=5 + K=3.
K=7: K=6 + K=4.
K=8: 3 x K=5.

Defining ‘some’ as 5 points, that becomes:

K=0: -5 END
K=1: -5 END -5 Stun
K=2: -10 END -10 Stun -5 Body
K=3: -15 END -15 Stun -10 Body -5 Stat
K=4: -20 END -20 Stun -10 Body -5 Stat
K=5: -30 END -30 Stun -15 Body -5 Stat
K=6: -45 END -45 Stun -25 Body -10 Stat
K=7: -65 END -65 Stun -35 Body -10 Stat
K=8: -90 END -90 Stun -45 Body -15 Stat

Or you could simplify things:

K=0: -5 END -1 Stun -0 Body
K=1: -10 END -5 Stun -1 Body
K=2: 2 x K1
K=3: 4 x K1 plus -1 stat
K=4: 8 x K1 plus -5 stat
K=5: 15 x K1 plus -10 stat
K=6: 30 x K1 plus -20 stat
K=7: 50 x K1 plus -30 stat
K=8: 100 x K1 plus -40 stat

The Healing Difference

It’s up to you to decide whether or not healing, or recoveries in the Hero System, can function until whatever-it-is has run it’s course.

That makes these effects much nastier and should cause you to halve whatever damage levels you had in mind. Unless you want it to be potentially deadly.

Other Systemic Options

There are five other options that the GM can choose. Some of these can operate in combinations.

1. The Exhaustion Option

When you roll a 6, after adding it to your tally, that dice no longer gets rolled.

That means that your biggest risk of a really bad result is at the start, and possible effects moderate.

It makes it much harder to predict the net outcome though.

Statistical Impact: This dramatically reduces the dice pool (N) over the course of the effect. Successes are achieved quickly, but the chance of rolling K>0 adverse events on any remaining die remains constant (1 in 6). Since the pool shrinks, the absolute chance of rolling multiple 1s decreases rapidly.

Game Feel: Front-loaded risk and rapid resolution. The initial rolls are the most dangerous. If a character survives the first two or three checks, the difficulty in rolling 1s drops faster than the difficulty in reaching the target, T.

Best For: Fast-acting, non-renewable poisons (like a single large dose of nerve agent) or short, focused challenges where the effect is quickly flushed from the system.

2. The Continual Option

Once you roll a 1, it stays unrolled thereafter and counts toward future penalties. Rolling continues until every dice shows either a 1 or a 6. The Core exit condition of accumulating T sixes remains in effect but is overshadowed by the alternative.

This means that things get progressively worse until whatever-it-is has run its course and left your system. It’s nasty but good for supernaturally-sourced troubles.

The one saving grace is the additional way out – if every dice is either a 1 or 6, the nightmare ends. In some cases, the cause – disease or poison – will burn itself out fast, in others it will be the cause of extremely protracted suffering.

The higher the initial N, the worse this gets. If you start with 6 dice:

1, x, x, x, x, x – T sixes (cumulative) or 5 sixes needed
K=1 events every roll until you roll another 1 or exit
1, 1, x, x, x, x – T sixes (cumulative) or 4 sixes needed
K=2 events every roll until you roll another 1 or exit
1, 1, 1, x, x, x – T sixes (cumulative) or 3 sixes needed
K=3 events every roll until you roll another 1 or exit
1, 1, 1, 1, x, x – T sixes (cumulative) or 2 sixes needed
K=4 events every roll until you roll another 1 or exit
1, 1, 1, 1, 1, x – 1 six needed
K=-5 events every roll until you roll a 1 or a 6. If you roll a 1, there is a K=6 events.

Each time a die is locked on ‘1’, your chances of getting the sixes you need go down and the number of rolls you’re expected to need will go up.

Damage accumulates very rapidly, and with accelerating pace.

3. The Progressively-worse Option

Each 1 that gets rolled increases the Target by 1.

This puts survival on a knife-edge and ensures that if you suffer badly, the effects will linger for longer – making it a good choice for plagues.

Statistical Impact: This maintains the dice pool (N) but increases the overall target (T) dynamically. Every adverse event makes the recovery condition harder to achieve. This means rolling a 1 directly increases the expected duration (E) of the effect. A single unfortunate roll early on can potentially double the total expected number of checks.

Game Feel: Cascading failure and desperation. Failure feeds failure. The character sees the light at the end of the tunnel (the target T) constantly moving further away. This is highly effective for plagues or diseases that exploit the body’s weakening condition.

Best For: Plagues, zombie infection progression, or effects that are harder to fight off the longer they persist (like a viral load).

4. The Blessed Balm Option

Sixes rolled can undo some of the harm caused. Two sixes = one 1, three sixes = 2 ones, and so on.

This creates a situation in which the health of the sufferer is on a roller-coaster, up and down with each roll of the dice. Eventually, these changes will tend to dampen out. Works very well with the Progressively-Worse option.

This fundamentally re-balances the risk assessment; introducing greater variance into the process – rolls are either great (success towards T) or terrible (a large number of 1s) or tension-building (anything else). It models a scenario where the character’s vitality is constantly tested.

Game Feel: Roller-coaster effect and high stakes per roll. The character may suffer a terrible wound but instantly cancel it in the same roll with a heroic recovery effort. This variation is highly dramatic.

Best For: Magical duels, effects that fluctuate with effort or willpower, and scenarios where the poison’s progression is inherently unstable.

5. The Devastating Option

The first 6 in a roll doesn’t count, only sixes above that one.

This strongly biases the results away from recovery, without ruling it out entirely. It makes any of the ‘nasty’ options far worse.

Statistical Impact: This increases the expected number of rolls (E) needed to reach T without changing the probability of adverse events (K). Since E is higher, the total number of adverse events over the life of the affliction is necessarily higher. If you use the same N and T, the effect will be substantially longer and more severe than calculated in the base tables.

Game Feel: Recovery – and the downhill slide before it – feels Incredibly sluggish and unforgiving. Successes are hard-won. This makes the affliction feel resistant or deeply embedded in the character’s system, guaranteeing prolonged suffering

Best For: Artifact-level curses, dire creature venom, effects designed to be a significant narrative roadblock, or spurs for quests for a cure. Don’t hit a PC with this variant except in unusual circumstances when they have no-one to blame but themselves; DO hit someone important who the PCs want to save.

6. The With-A-Bang Option:

A selected number of the dice pool (N) start already showing ones and are not re-rolled. These reduce by 1 each round, becoming regular dice rolled and not “fixed ones”.

The “Fixed Ones” should be 1/2 of N or less. This ‘forces’ the occurrence of a high K result in the first round, tapering off in subsequent rounds. It also extends E by reducing the likelihood of sixes being rolled, generally by the number of fixed ones at the beginning, minus 1.

6a. Bigger Bang Sub-variant

The”fixed ones” are only removed when a 6 is rolled. A 6 used for the purpose does not count toward the target.

This extends the durability of the high-N count AND effectively increases T by the number of initial ones showing.

6b. It Will All Be Over Soon Sub-variant:

As per the basic option 6, but fixed ones do not become regular dice, they become automatic sixes.

This front-loads the results with high-K results but effectively reduces T by the number of initial ones showing.

Going Further

Any situation in which one character uses his skills to solve a multipart problem, or a group collaborate on a challenge, or a group face adversity together, or that can otherwise be broken down into units of roughly equal value, can be modeled using the Adverse Effects Engine.

Each part of the problem, or contributor to a solution, or participant, gets one dice, and they all roll collectively at the same time. This is especially powerful when coupled with the variants listed above.

Think of T as Progress, N as Resource/Skill, and K as Consequence (usually Immediate, but that depends on the definitions of harm that you set up).

Here are just a few of the many situations that the engine, correctly configured, can simulate.

Extreme Weather

N = number of PCs / NPCs in the group

T = N unless there is a natural channel either guiding the weather toward them (+1-3 T) or away from them (-1-2 T).

K = scale of impact of the weather event on the group.

Best Option: The Blessed Balm PLUS Progressively Worse:
Each 1 that gets rolled increases the Target by 1.
Sixes rolled can undo some of the harm caused. Two sixes = one 1, three sixes = 2 ones, and so on, mitigating an existing K result OR reducing the Target by 1 if there are no K results to mitigate.

Everybody rolls a dice and contributes the result to the roll. Sixes push the weather away from the party, Ones bring it down on top of them to a degree. Net effects change from round to round, with weather either just missing the characters (K=0), catching them at its fringes (K=1), or enveloping them (K>1).

For added flavor, throw in Nested Damage Types – First impact = Wind, Second impact = Rain / Hail / Snow, Third impact = Stronger Wind, and so on.

Product Development

Your PC is part of a team developing a new product for sale. You will need a Market Specialist (salesman), a production / manufacturing engineer, a marketer, a technical expert, and a team manager.

The salesman will identify a gap in the market to be targeted, the technician will design the product to fill that gap, the engineer will determine what the possible price-points are, and the rate of production that is possible, the marketer will figure out how to sell the product, and the team manager will make decisions and look at the costs of altering the production environment to change the production engineer’s forecasts.

Each team member gets at least 1 dice to contribute; if their specific skill is more than double the lowest specific skill in the team, they get a second one. If the company has a good history / reputation in the field, the GM can award 1-3 extra dice.

T starts at 1 per team member. If the company has a bad history or reputation to overcome, add 2. If the product is especially cutting-edge, increase this subtotal by +50% or even +100%. If the market is especially cut-throat, add another 25% on top of that. For each team member whose specific skill is less than half the highest specific skill amongst the team, add another 1.

Each 6 counts +1 towards the product being fit for purpose. Each roll marks a milestone in the development process – there can be blind alleys, competitor announcements changing the market / playing field, cost increases, new markets opening up, old markets closing down, scandals in the boardroom – anything and everything that affects the market for the product.

Penalties take the form of additional design time between rolls (K=0, K=1) and reductions in the fitness for purpose of the resulting product (K>0).

I don’t think any of the optional configurations are appropriate for this application.

Collaboration to overcome an environmental hazard (1)

Use the AEE for ongoing natural challenges where the group’s collective effort determines the duration, and individual poor luck determines the immediate suffering.

Crossing a Frozen Lake or Glacier, for example: N (Dice) = The number of characters in the group, or the lowest relevant skill rating in the group, or some reasonable fraction thereof. Only characters with a relevant skill or with a relevant stat value higher than a medium-high threshold get a die. Below those marks, the characters are liabilities toward the group’s success.

T = the GM-assigned difficulty, or some simple fraction thereof, +1 per character, whether they get a die or not..

Options Configuration: The Continual Option, PLUS The Blessed Balm Option.
Once you roll a 1, it stays unrolled thereafter and counts toward future penalties. Rolling continues until every dice shows either a 1 or a 6. The Core exit condition of accumulating T sixes remains in effect but is overshadowed by the alternative.
Sixes rolled can undo some of the harm caused. Two sixes = one 1, three sixes = 2 ones, and so on – removing it from the locked pool and releasing it back into the live dice to be rolled.

Collaboration to overcome an environmental hazard (2)

The party are roped together and have to climb.

N = Characters with climbing skill of +2 or better, or STR+DEX of 16 or better.

T = Total number of characters + 1-4 for difficulty of climb. Add 2 if the characters are under attack or otherwise pressured to climb at speed.

K = falls / setbacks. K>2 = ropes break.

Options Configuration: The Exhaustion Option simulates the rope tying the bad climbers to the good ones: When you roll a 6, after adding it to your tally, that dice no longer gets rolled.

For especially difficult climbs, add The Progressively-Worse Option: Each 1 that gets rolled increases the Target by 1.

For the most supremely challenging climbs, add the Devastating Option instead of Progressively Worse: The first 6 in a roll doesn’t count, only sixes above that one.

Ransacking A Library for specific (hidden / obscure) information

How long it takes to find a specific piece of hidden or obscure lore in a Library that might not even contain what you’re looking for depends on your reading speed (INT), presuming you have the ability to read, and your ability to recognize what you’re looking for, or that what you have just found is a clue to where to look next.

Well-structured libraries also make it a lot easier by excluding most of the books as irrelevant.

I would employ a simulation similar to the Design-A-Product example, but based purely on INT and not on specific skills. Note that if you have a character participating who is low INT, they can actually disrupt the efforts of higher-INT characters by continually interrupting them with “is this it?”.

Specifically, you want the total number of 6s to exceed the total number of 1s before the search comes to an end. If it doesn’t, either the answers aren’t there, or you’ve missed them. So long as there are dice to be rolled, there’s a chance, even if you’re at -2 or -3 to getting a result.

K=penalties to the success total, high-K = passing guards, accidental fires, magical books that scream when opened, ghostly librarians…

Focal Character overcoming an environmental hazard

All sorts of things fall into this category. Picking a combination lock, for example. Or Disarming a bomb with N critical steps that have to be performed in the right order. Or using a code-breaker.

You’ve seen these devices in the movies. Attach one to a lock and let it work its way through the combinations. To make life more difficult, consider a rolling code – that’s where a complex algorithm sets a new code every time, but only the 1000 or so valid results from that algorithm will be accepted. Which means that if you lock in the wrong answer, you have to start over.

The relevant skill here isn’t necessarily one of yours – it’s the design and programming skill of whoever designed and built the code-breaker. All you have to do is place it on the lock in roughly the right position.

With each success (each 6 toward the T), the stakes get higher. One wrong move (K>1) and it’s back to square one.

This scenario seems tailor-made for the Exhaustion Option – a 6 is a locked-in digit: When you roll a 6, after adding it to your tally, that dice no longer gets rolled.

Lesser K results are events that threaten failure / discovery, but which may not actually incur the problem.

T=Number Of Digits in the code.

N=T+a simple fraction of the programmer / designer’s skill.

Let the tension build…

Using The AEE

If you prep in advance, you have plenty of opportunity to consult the tables and simply put the specific simulation instructions into your notes.

If you want to be able to use the system off-the-cuff, though, you’re going to have to be able to take it with you. For that reason, I’ve put together a PDF with the essential mechanics, shorn of explanation and example – but WITH a hyperlink back to this article.