Image by PIRO from Pixabay, cropped by Mike

The December Blog Carnival by Rising Phoenix Games is on the subject of “No Dice“. This is the beginning of Campaign Mastery’s contribution to the subject.

There are times when it can be useful to the GM and his simulation of reality not to require a roll for something. This article is going to explore the conditions under which that seems worth considering, and what the resulting game mechanics mean in terms of that reality.

The Basic Approach

Just to be explicitly clear on what this article is going to propose, I thought it would be useful to set a baseline describing the usual process and what the rolling of dice normally represents in terms of underlying internal game physics.

While I can’t state that these interpretations will be correct for all game systems that use die rolls, I’m going to keep this at a level such that it will apply to the vast majority of game systems. To achieve that, I’m going to make sure that the interpretations provided are valid for the Hero System and GURPS, for D&D and Pathfinder, and for both my Doctor Who campaign (which uses The Sixes System and my now-completed Zener Gate campaign (which uses its own bespoke rules system. .

These systems are so different in their mechanics that the results should apply broadly to almost every RPG out there, with the occasional exception.

In particular, for each stage of the conceptual framework, I’m going to look at seven specific circumstances:

• Skill Checks
• Stat Checks
• Perception / Sensory Checks
• Saving Throws
• Attack Rolls
• Damage Rolls
• Rolls for effect

You’ll note that I’m explicitly including Saving Throws even though not every game system uses them; when a game system doesn’t, it usually substitutes some sort of stat check for the save mechanics, but the interpretations and implications can be quite different.

It might grow complicated at times, because some of these interact. For example, rolled attacks but not rolled damage, or vice-versa. I’m going to try to avoid this as much as possible, but there will be some of these fringe questions along the way.

Rolling Skill Checks

There are two basic kinds of skill check – knowledge checks and ability checks. Knowledge checks can include how to do something with a practical skill.

• Does the character know the answer to the question being posed? Can he solve the problem, or at least get a step closer to a solution? Can he devise a theory, and a way to test that theory? Can he spot the flaws in a plan or in someone else’s theory?
• Does the character recognize this architectural style? Can he determine which columns are load-bearing and which could be hollow?
• Can the character successfully attempt to do something, like repair a net, or patch a boat hull? How long does he think it will take to forge that sword?
• How much will it cost? What does the character consider a fair price for his services? If an NPC is to do the work, does the character think the price is reasonable?
• How good is the character at working with the tools available – and can he improvise his way around the lack of such tools if he has to?

These are all skill checks. The basic concept embedded in most RPGs is that there are all sorts of variable factors and an element of random chance in most of these tasks, and simulating those factors is the job of the die roll in such a check.

Rolling Stat Checks

Stat checks are very similar, but they deal with the more elemental raw abilities. In many game systems, if you don’t have an appropriate skill to fall back on, you can default to the raw stat check, the innate capacity to work in the field – sometimes with a penalty to you chances of success.

But there are also occasions when no skill is as relevant as those innate capacities. Holding your breath, for example, or running over broken ground, or holding onto something slippery.

If you assume that the stat value provides and defines the unskilled capability of performing such an action, then the die roll takes into account all the variable factors, just as it does for skill checks.

The other function of stat rolls in most game systems are opposed rolls. A tug-of-war is a typical example, in which each participant attempts to apply their strength more successfully than the other. But the same concept applies to attempts to persuade someone – assuming you don’t have a skill that applies, and to all sorts of other interactions, like bartering.

The rolls don’t have to be like against like, either. One stat might represent that character’s natural ability to sneak, while the opposing stat would be that character’s ability to perceive hidden objects.

Again, the stat represents the innate potential of the character, the die roll integrates that potential with the circumstances and variable factors to determine how well the character is able to apply that potential.

Attention and Awareness

‘Make a perception roll” – or it might be a Spot Roll, or a Listen check, or any number of alternatives. But they are all sensory checks, when you get to the bottom line. I could spend an entire column on this subject, but that would take us way off the point.

So here is the very-abbreviated version. When something happens, there is usually a visual change in the environment, or an audible change, or an odor, or – sometimes – a particular taste in the mouth. But for that change to impact on the character’s awareness, they first have to notice the change and then to correctly interpret it, and then recognize the significance. And none of that is as easy as it sounds.

Confirmation Bias, Ideation & Fixation, Malleable Memory, Illusions, Deceptions, and at least half-a-dozen other phenomena are all able to get in the way. Spend too much time looking into, for example, the reliability of witnesses, and you’ll find yourself starting to wonder if any of us ever really see anything clearly.

One truism is that the more attention we pay to something, the better we remember it, and the more details about that something we will typically notice. This usually comes at the expense of awareness of anything outside the scope of that something, and in extreme cases, complete obliviousness to even attention-getting phenomena like alarms and sirens and what other people are saying to us. That’s called fixation, and it’s one of the items on that list above.

Another factor is the state of mind of the witness, which can rewrite perceptions or cause them to be wildly misinterpreted.

In terms of the game mechanics that usually apply, not only do we have to be paying attention to the right thing in the world around us, our awareness has to navigate that whole litany of perceptual errors to bring it to our attention. All of which gets collected into a big conceptual pot called a die roll.

If you fail a perception check, it doesn’t necessarily mean that there was something to see and your didn’t notice it, in fact that’s going to be the case no more than 25-50% of the time. The rest of the time, one of those perceptual or cognitive traps intercepts the awareness and misinterprets it.

So you can interpret a perception check as a means of overcoming these deficiencies, and that would be as valid as any other interpretation..

Rolling Saving Throws

     “A whistling sound fills the air as a spark leaps from the spell-caster’s outstretched hand, flies up to a few dozen yards in height, and begins to fall toward you.”
     “I throw myself to the ground and search for any sort of cover I can find!”

That’s the usual interpretation of a Reflex save. Some GMs may omit all of the above and simply have the player make a Reflex save to throw themselves flat on sheer instinct, as – in fact – a reflex action.

The other kinds of saving throws that are common also derive from D&D: Fortitude saves to resist various things that could distract or incapacitate a character, and Will saves to resist various things that could influence or control their minds.

But, even though this iconic trio stem directly from D&D, most game systems have some sort of equivalents. Sometimes, these are run as stat checks like any other; that is especially common in game systems that don’t have the artificial construct of ‘character levels’. In fact, it’s fair to say that the only reason these checks are semi-divorced from stat scores is to permit the character level input to be the dominant factor.

Is it enough? Is it done in time? Do random factors – like what you had for breakfast – work in your favor? All such considerations are encompassed by the die roll component of a Saving Throw.

What about Modifiers?

If the random die roll is supposed to take all the ‘wild variables’ into account, what, then, is the role of Modifiers to these rolls? Before I move on to attack rolls, I thought it worth taking a moment to discuss modifiers and what they should be considered to represent in the game reality created by the rules system.

Most saving throws and stat checks can be assumed to incorporate those random variables into the die roll, assuming typical circumstances and an even positive-negative influence.

When either of these is not the case, modifiers should be used to reflect that. Effectively, they bias the die roll to take into account unusual circumstances, abnormal difficulties, and other forms of strangeness.

I use bonuses to reflect things like distractions, confusing environments, deceptions and ruses, distance, minuteness of pertinent details, the adequacy or inadequacy of the tools available (if such are necessary), and so on.

I also use them to compare the difficulty of the challenge / question relative to a character of similar skill to that of the character – because a character with a reasonably good skill level should be able to answer basic questions at least 9 times out of 10. Similarly, some problems are going to be harder for anyone but an expert to solve.

The latter is less relevant to game systems like D&D in which a certain natural result on the die always succeeds. because this overrides the consequences of the bias. In the Zenith-3 game system, there are no automatic successes, but there are critical results; “00” is read as “oh-oh” (checks are on d%), and means that something has gone wrong, any failure will be worsened and any success minimized or nullified outright. In fact, it usually signals a reverse of some sort. “01”, in comparison, is read as “Oh, Wow” and means that successes are enhanced, failures are diminished, and so on.

The Plotting Value of Bias Metagaming

Sounds fancy, doesn’t it? This simply means deciding what you want the chance of success to be in a given situation, determining what bias is necessary to translate the character’s normal roll into that probability of success, and then ‘delivering’ the circumstances needed to justify or create that bias.

Or to put it another way, you determine how difficult progress should be for the PC(s) in question and introduce plot elements to achieve that metagame outcome.

When you do this, you always need a ‘Plan B’ for the players to follow, even if they don’t know what it is; where there is one solution, there are probably several. Such metagame roadblocks exist to steer the adventure in the direction of more fun; there should be no malice involved.

The goal is for everyone to have fun. But that doesn’t mean letting the players always have their own way; it does mean rewarding them with success when that’s justified.

The Gods Are Watching

One more sidebar before returning to the main text. This is also metagaming, but in a positive way. Sometimes, especially in temples and the like, the Gods are watching, and may choose to help or hinder; instead of a random die roll to determine this, and then translating that result into a bias on the actual check, I assume the Gods have been watching and judging the characters as they approached this point.

If the Gods would have a good impression, that translates into a positive bias that the character can’t explain; if not, a negative one. And I do take into account how well the character was being roleplayed. Do that well enough, and even an enemy might develop a grudging respect for you – enough to stay their hand when they would be normally inclined to bias things towards trouble for you.

Attack Rolls

Attack Mechanics tend to work in one of two ways: the instant and aggregate time.

D&D and related systems are ‘aggregate time’ mechanics. Each ‘attack’ combines several thrusts, parries, swings, bobs, weaves, and dodges, all probing for an opening in the defenses of the target while keeping yourself clear of enemy attacks. But GMs rarely describe combat that way, and even less frequently, think about it that way.

Superhero games, in particular, tend to be have ‘instant time’ mechanic, in which each move and countermove is determined individually. That’s a reflection of the expected impact on the combat setting; even a single missed attack can have major repercussions.

Other game systems can use either of these interpretations, often without ever spelling out the assumptions that underpin their simulation of ‘in-genre reality’.

The difference is important, because the meaning of the die roll component of an attempted attack is different in both cases.

In ‘aggregate time’, it’s the conflict between maneuvering your opponent into a misstep while presenting minimal opportunities yourself, compounded with your capacity to exploit such mistakes. The die roll is a direct reflection of your success at doing this.

In ‘instant time’, such maneuvering is no longer treated as a collective series of events, and is therefore under the direct control of whoever is running the character. There is no luring of an opponent into a mistake; instead, it’s all about how effective an attack is at penetrating or bypassing the target’s resistance to that attack. In some ways, this can make the combat more interactive and hence more exciting; in others, it can slow it down enormously. There are vastly more variables and parameters that get aggregated into an ‘attack roll’, things that the ‘aggregate time’ perspective simply glosses over. If more of these random factors align in your favor, you are successful; if not, you are not. So that’s what the die roll component represents in such systems.

Many of these systems (especially the hero games system) use 3d6 for attack rolls. Any system that uses multiple dice for such rolls is mapping probabilities to a familiar pattern, the bell curve. The reality of such curves is that they can be viewed as being all about the deviation from the mean – a singularly appropriate perspective, under the circumstances.

Damage Rolls

Most game systems have a separate roll for damage, meaning that the attack roll does not represent the quality of success of the strike, only that it has been successful. The damage roll therefore represents the effectiveness of the attack.

In some game systems, this is the net effect; in others, this is a preliminary value that is then reduced by other game mechanics. The difference is a logical consequence of the differences in attack roll interpretation, i.e. ‘aggregate time’ vs ‘instant time’.

In ‘aggregate time’, the attack roll incorporates a host of modifiers to determine the overall consequences of multiple attempted attacks. This logically includes all the target’s defenses; hence there is no need to account for these in the damage roll, so the damage rolled is a net value.

One of the frequent complaints heard in the early days of AD&D was that this was unrealistic, and reduced the value of defenses more than should be the case, especially since attacks improved with rising character levels but defenses did not, and I have to concede the validity of the last point, at least. Character defenses were, as a result, one of the most common house rules offered – most of them missing at least one key point.

Rather than modifying the amount of damage done by having defenses increase with character levels, these game systems increase the capacity to absorb damage with character levels. In effect, the results make the damage done, as a percentage of the total to be endured by the character, smaller with increasing character levels. The significance of this was often not appreciated in the debates mentioned above, which formed a second nexus of debate because character classes did not increase in capacity equally.

It’s not the place of this article to try to resolve these debates, or even assess whether or not they remain relevant. My scope here is simply to provide understanding of what the variable element, i.e. die rolls, are simulating in such game systems.

When the game system uses ‘instant attack’ resolution, the same compromises are neither possible nor all that desirable, and that permits more realistic damage handling systems – including defenses that modify the amount of damage done.

Rolls for Effect

The final category covers rolls for effect. These are usually from spells or paranormal powers. In ‘instant time’ game systems, they tend to be relatively fixed in value, only increasing as a result of specific decisions in ongoing character development.

In ‘aggregate time’ systems, they tend to increase with character levels, with some exceptions for character class levels that are deemed to follow a different character track. That’s the difference between ‘Caster Level’ and ‘Character Level’ in such systems.

This lay at the center of a third nexus of debates amongst AD&D GMs and players, largely because they didn’t appreciate what the increase in character hit points was supposed to simulate. The reason relevant spells increase in effectiveness with caster level is not to make them more powerful, it is to maintain an approximate parity with rising hit point levels in targets with increasing character levels.

Because this context was not understood, the increase in the number of dice rolled for effects was not understood, either, and that led to a number of half-baked house rules at the time. The only consolation is that there were fewer of these house rules that made it into the game magazines, acquiring some level of semi-official plausibility in the process.

The biggest problem with most of these house rules was that they weren’t comprehensive and holistic; they focused on one specific element of the system without considering the big picture or how the elements of the game mechanics were supposed to integrate, and as a result, they tended to miss the mark.

Be that as it may – most effect determinations involve some sort of die roll, usually on multiple dice.

And when you are talking about multiple dice, you are talking about bell probability curves – the more dice, the more results will tend to cluster around the average result. For another article some time back, I produced the diagram below to illustrate this point.



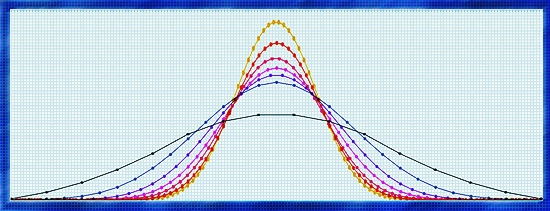
Just to be complete about illustrating the ‘shape’ of effect rolls, below is a set of images from the series describing the sixes system that addresses the impact of rising numbers of d6:



The middle set of graphs shows the same thing as the stacking of d6 graphed above this trio but in less detail.

So, what does all this variability represent?

I have to admit this is the hardest thing to get your head around. Superficially, it looks like the only reason is to insert unpredictability into the system.

To really understand, you have to make a deep dive into the actual consequences of increasing effect dice in a numeric sense. There are consequences of note:

1. Minimum possible results increase by one per die added to the roll.
2. Maximum possible results increase by the die size per die added to the roll.
3. The probability range clusters more tightly around the average result.

The last one is the hardest for people to understand in a quantitative sense; it’s relatively easy to get a handle on the concept, but much harder to get a ‘feel’ for how significant it is.

To try and deliver an appreciation for the impact of the clustering, I’ve considered a number of different die rolls below, using Anydice, which was also employed for the graphs above.

I’m setting the technical details of the graph into this sidebar as they won’t matter much to most people.

Starting with the result or results of greatest probability, I totaled the probabilities, spreading out to either side. This enabled me to determine the range of results that equated to a given likelihood, and the results were then compiled into the table that follows the curve.



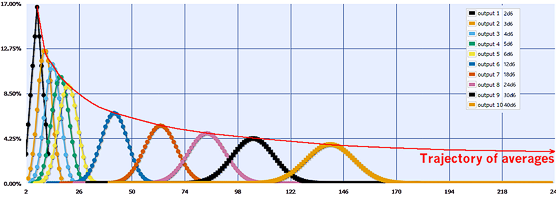
That’s useful in an illustrative way, but not helpful beyond that. The analysis is more revealing.
 

% of results	Number Of Dice
	2d6	3d6	4d6	5d6	6d6	12d6	18d6	24d6	30d6	40d6
3%										140
4%									105
5%							63	84
7%						42
9%					21
10%				14					104-106	139-141
15%	7						62-64	83-85		138-142
25%		10-11			20-22		61-65	82-86		137-143
30%			13-15			40-44		81-87	102-108	136-144
35%							60-66		101-109
40%	6-8	9-12		16-19	19-23	39-45		80-88		135-145
45%							59-67		100-110	134-146
50%			12-16					79-89	99-111	133-147
55%				15-20	18-24	38-46	58-68	78-90	98-112	132-148
60%							57-69	77-91		131-149
65%						37-47			97-113	130-150
66.67%	5-9	8-13	11-17
70%				14-21	17-25	36-48	56-70	76-92	96-114	129-151
75%							55-71	75-93	95-115	128-152
80%	4-10	7-14	10-18	13-22	16-26	35-49	54-72	74-94	93-117	127-153
85%					15-27	34-50	53-73	72-96	92-118	125-155
90%	3-11	6-15	9-19	12-23	14-28	33-51	51-75	71-97	90-120	122-158
95%			8-20	10-25	13-29	31-53	49-77	68-100	87-123	117-163
97.5%										100-180
98%							47-79		84-126
98.5%				9-26	12-30	28-56	46-80		83-127
99%					11-31	27-57	45-81	63-105	82-128
100%	2-12	3-18	4-24	5-30	6-36	12-72	18-108	24-144	30-180	40-240

 

The color bands divide the table up into 1/3 of the results, 2/3 of the results, and more than 90% of the results. And, at the last minute, I threw in a row for 100%, just to be pedantic.

The table shows that on 3d6, two-thirds of your results will typically be from 8 to 13. On 12d6, 70% of your rolls will result in results between from a low of 36 to a high of 48. And, on 24d6, 90% of your rolls will have a result from 71 to 97.

If you look again at the graph, you’ll note that a lot of results have virtually zero change of occurring. Never quite zero, if they are within the theoretical range – you can still roll a 34 on 30d6 – but it’s exceptionally unlikely.

This shows the real impact of the narrowing of the bell probability curve relative to a lower-dice curve. One third of results on 40d6 will fall within a span of 11 numbers – 135 to 145. More than two thirds will fall within a range of 23 numbers – from 129 to 151. 95% of the time, 40d6 will yield a result somewhere between 116 and 164, a span of just 46 results – and a far cry from the full 40-240 range.

I doubt that many game designers performed such calculations, at least in the early days – there was too much spit and baling wire in the rules-creation process back then, too much seat-of-the-pants and ‘that looks about right”.

But the ultimate goal remained – raising the minimum and maximum effect and making a ‘reasonable’ result more likely, relative to the rising hit points of enemies as they went up in terms of the challenge that they posed..

Still a long way to go in this article, but I’m right out of time, so I’m going to have to split it into at least two, and possibly three, parts. Come back next week to get the next installment!