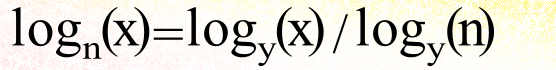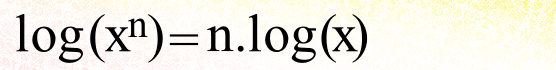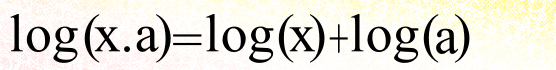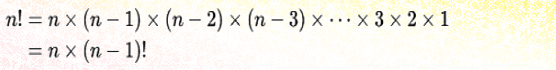Image by Gerd Altmann from Pixabay

I came across a remarkable mathematical fact the other day, which immediately gave me the idea for this post.

Yet, while I noted the fact, and roughed out a structure for this article, when the time came to actually write it, the gaming relevance that had been so obvious and self-evident that I had not written it down completely escaped me!

I can only hope that by the time I get to the end of my notes, it will have come back to me!

Introduction / Preface

I should begin by thanking Peter-3699 of Quora, who posted the remarkable mathematical fact that inspired this article – I’ll link to it when it becomes relevant.

Every non-Wikipedia link in this article is either from him or from a comment to his post, or from a page so linked, and so (arguably) would not exist without his post.

Any readers with visual impairment should note that I have gone to some trouble to quote most of the mathematical formulae discussed in this article as Alt-text, so you won’t be left out. I can’t make it any easier for you, I’m afraid, but I hope that it will be better than nothing.

The remarkable property of Pi

The properties of Pi have long fascinated mathematicians – it is what is called a Irrational Number, a number with a never-ending number of decimal places that never repeat. There are a boatload of these known to maths these days. An irrational number is one that can’t be precisely defined as a fraction of two whole (integer) numbers (though approximations are possible).

It’s conjectured (and widely believed) that the various decimal digits (0, 1, 2, and so on up to 9) are evenly and randomly distributed, but this has never been proven.

Pi is one of the earliest constants known to reflect a physical property of our reality – the Circumference of a circle is 2πr and it’s area is πr².Those mean that the properties of cylinders and spheres also use π. But π shows up in trigonometry, and electrical formulae, and in formulas about spings, and all sorts of other places, too.

When I was a young high-school student (aged 12 or 13), I was fascinated by two facets of pi and spent many hours attempting to understand them.

The first was inspired by my discovery that you can get the logarithm to any base by dividing the logarithm in a known base of the number desired by the logarithm in that same base of the desired base. Spelling it out in words is not as elegant as showing it as a formula:

I routinely use y=10.

I’ve found this to be useful in RPG rule analysis and construction many times, mostly for bases of 2 and 5.

(Another pair of formulas of value, while I’m in the vicinity of the subject, are

It doesn’t matter what the base of the logarithm is so long as it is the same both times.

…and…

It doesn’t matter what the base is so long as it is the same in all three cases.

At the time, though, i didn’t even know that RPGs existed (and to be fair, at that time, they didn’t exist in any form that we would now recognize, this was the mid-70s). Instead, I was captivated by other concepts.

I already knew that logarithm bases could be irrational, having discovered a reference to natural logarithms (logs to the base of e, which is physical constant defined as approximately equal to 2.71828. (e also shows up in all sorts of unexpected places, for example in modeling compound interest). In fact, it’s relevant to all sorts of exponential growth and decay, including half-lives and biological population growth.

But I couldn’t find anything anywhere about logs to the base of pi, and whether or not this was a useful or practical concept. Short answer – it is, but perhaps less than you might think.

The other question was inspired by a Scientific American whose cover story focused on attempting to find patterns in various geometric representation of the distribution of prime numbers, or the results of plugging prime numbers into various formulae such as n=(P(a)-1)/2, or n=[P(a) – P(a-1)] (where P(a) is a given prime number, like 11, and P(a-1) is the preceding prime number.

Aside from being fascinating in and of itself (and endlessly time-consuming), I wondered if there was some relationship between the digits of an irrational number like pi and the distribution of prime numbers. Instead of a lattice for example, what if the numbers were organizes in growing concentric rings with 0 or 1 in the center?

Short answer: I could never find one, but that doesn’t really prove anything. It was a fun diversion, though.

Quite obviously, there have been many and ongoing attempts to calculate pi, first for its practical value and second because it’s nature makes it a gateway drug into some of the most abstruse realms of higher mathematics.

Babylonian mathematicians usually approximated the value to 3, which was good enough for the archaeological projects of the time. This value was also used in astronomical calculations in India. By the 6th century BCE, Indians were using 339/108 as an approximation.

A thousand years earlier, in a text that was itself stated to be a copy of an even older document in ancient Egypt, the same fractional approximation of 339/108 was described.

Archimedes proved that pi lay somewhere in between 223/71 and 22/7 using geometry of regular polygons within a circle, which would give a circumference of ever-increasing accuracy with more ‘faces’ or ‘gons’ (“poly” means “many”, so “polygon” means “many gons”). For some unknown reason, he stopped at a 96-sided polygon even though his technique required only patience to be extended a considerable distance further.

So, pi is important, and that has led to many attempts to calculate it, to get back to the point.

In fact, the Pi Formulas page of Wolfram Mathworld lists no less than 135 different formulas for calculating Pi! Most of them are too exotic to explain here; I’ll get to some of those that are not in that category in due course.

But this answer on Quora got me thinking about the nature and representation of decimalized numbers…

Whole Numbers

The simplest such numbers are whole integers, with no decimals to worry about at all. The approximations of pi as “3” are representative of this. (Integers, when you dig into them, can be just as fascinating as irrational numbers. For example, there are an infinite number of them, but for every single one of them, there are an infinite number of numbers that aren’t integers – which is a gateway into the very strange world of the mathematics of infinity.

Simple Fractions

As soon as you come up with the concept of measuring some objective reality, you start discovering the world of simple fractions. For example, if you have an object of a particular length, the midpoint is found by dividing that length by 2. If the length as measured happens to be evenly divisible, this is easy; but if it is not, you end up with either a remainder (not useful) or a fraction, 1/2, included in the answer.

Divide something into 3, and you get the fractions of 1/3 and 2/3 being defined, and so on.

Some fractions that are technically “simple” go beyond what I would consider “simple” in an everyday interpretation of the word. “22/7” is simple in both interpretations, and is perhaps the simplest real approximation of pi; the fractional approximations given earlier, like 339/108, may technically be simple, but are pushing the limit of the everyday sense of the word.

Fractions are inherently bound up in geometry and lead into angles and trigonometry. But they remain a finite tool until something else is added to the mix: the invention of a zero.

The Invention of Zero

Zero makes positional notation possible. Without it, you can’t have decimals. “10” is positional notation; the position of the “1” is meaningful, with the character ‘0’ being used to describe that position.

Ancient Egypt had a zero concept for use in accountancy, but did not use positional notation; each number was represented by one or more hieroglyphs. The ancient Babylonians came close, with a symbol used as a placeholder for a zero in their base-60 system.

Modern representations of time that would be familiar to all readers – 3’59” for example – preserve this base-60 system, with 60 seconds equating to a minute and 60 minutes to an hour. The symbols ‘ and ” identify the significance of the 3 and the 59 that – in this example – precede those symbols, respectively. This is a somewhat more refined version of the Babylonian system.

The ancient Greeks had no symbol for zero, and no positional notation. In fact, Greek philosophers opposed the concept of zero as a number very strongly for a very long time, going so far as to translate their numbers into the Babylonian number system for calculations and then translating the results back into Greek to give their results, just so that they could avoid contaminating their number system with those pesky zero-equivalents. Ptolemy broke with this trend and started using a zero-symbol as both a placeholder and a digit, but this did not catch on.

So it was that ancient Romans weren’t able to inherit a zero from the Greeks, and the whole Roman Numerals thing happened instead. “MMCCCXVI” is partially positional (the “V” and “I” mean different things depending on their order, and “IX” applies this to the “I” and the symbol for 10, “X”). But M, C, and X were not used in a purely positional manner; instead, each represented “one” of whatever units were used. So “MM” stands for “two thousands”, and “CCC” for “three centuries”. “MMCCCXVI” is “2,316”. Romans did have a digit that represented “no remainder” after mathematical division.

Slowly, the twin concepts of zero and positional notation within numbers were built up by different societies until a Persian mathematician synthesized his own mathematics from Hindu, Greek, and Arabic sources, unifying concepts from each into a single structure of numbers. The word “Algoritmi” was the Arabic translator’s Latinization of Al-Khwarizmi’s name, and has developed into the modern word “Algorithm”. Al-Khwarizmi wrote (and taught) that “if no number appears in the place of tens in a calculation, a little circle should be used ‘to keep the rows’.: This circle was called Sifr, and it was in every practical respect the forerunner what we know of as zero today.

From these beginnings, the concept of zeros and base-ten mathematics spread to Europe by way of the Spanish Moors, and in particular, Gerbert of Aurillac, and it is from his name that the term “Arabic numerals” derives.

Mathematical calculations prior to the zero were at the level used to teach basic arithmetic to kindergarten children and other early-year students. When I was going to school, the highest form of such math was the memorization of the times tables; which used rote learning to embed concepts into applied mathematics without explanation for why numbers worked the way they did. But the fact is that every advance in arithmetic above elementary addition, multiplication, division and subtraction only works thanks to the zero and the positional notation that it makes possible.

Simple Decimals

Once you have zero and positional notation, you can have simple decimals, essentially writing a number like “2 and 3/10ths” as “2.3”, and a number like “4 tens, 3, and 57 one hundredths” as “43.57”.

Non-repeating Long Decimals

Somewhere beyond two or three decimal places, you enter the realm of “Long Decimals”. These are numbers that include fractions whose decimal conversion can be fully shown, no matter how long and complicated. “Ten thousand Seven Hundred and Forty Two one millionth 48 thousandths and 576ths” can be written “10742 / 1048576” as a fraction, or 0.0102443695068359375. For convenience, long fractions sometimes use a space after every third decimal point, just as “1048576” is sometimes written “1,048,576” – so “0.0102443695068359375” becomes “0.010 244 369 506 835 937 5” – but this decimal representation is the exact number represented by that particular fraction.

Simple Repeating Decimals

Long before you’ve worked these out, however, you have discovered simple repeating decimals. “1/3” is the simplest of these – it’s 0.333333333333… and the decimals continue on indefinitely.

One quarter and one fifth don’t have these properties, but one-sixth does – 0.166666666666666… and so does one ninth, or 0.11111111111111… and, in fact, every fraction whose denominator is evenly divisible by three. So one seventy-second is “0.01388888888888…”.

These are frequently denoted by putting a dot on top of the decimal place that is repeated – so:

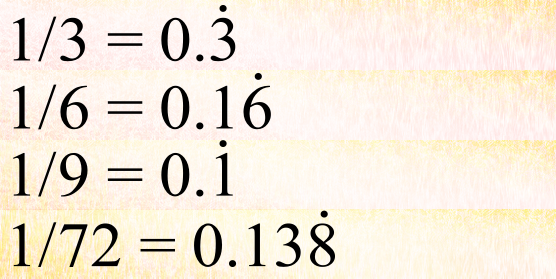
Complex Repeating Decimals

One seventh is even messier, as are any fractions whose denominators are evenly divisible by 7. One 63rd, for example, is “0.015873 015873 015873 015873 015873…”, in which a string of 6 decimals is repeated an infinite number of times.

These are usually written with a dot over the first and last decimal in the repeating string, so

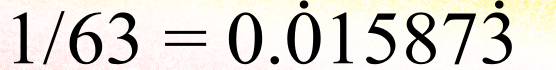
These clearly represent a whole new order of complexity when it comes to decimals, but we’re still not at the complexities represented by the digits of pi.

Non-Repeating Decimals as Fractionated Series

And that brings me back to the answer on Quora by David in response to the question, Can π be expressed by a series?.

In response, Peter offered up the following simple series:

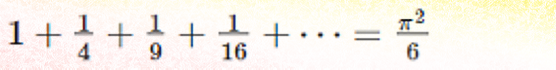
But I think it becomes even more obvious when written,

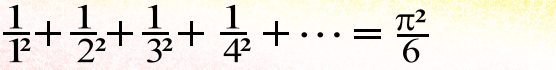
I had encountered a few of these before, but they were more complicated. For example, there’s this one:

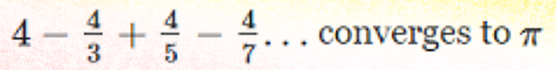
The primary source referred to by David, the Pi Formulas page of Wolfram Mathworld, as mentioned earlier, has a great many more. The series listed above is almost as elegant as David’s (only the addition-subtraction perpetual series prevents it from equalling that mark). There are others that are a lot more complicated.

These define a number not in terms of its actual value, but in terms of a process that can be used to calculate it. The problem is that to extend the number of digits of pi, you have to calculate every term up to the depth of your required decimal places, and the number of terms to be calculated grows faster than the decimal places do.

For example, in the formula above, it’s a sure bet that eventually, you will get to 1/81 – that will be somewhere around the 40th term. But 1/81th is 0.012345679 012345679 0123456790… – so that’s 40-or-so terms and we’re still only on the second decimal place!

There are some formulas that converge more quickly on pi; for example, this one…

Observe that this is simply a more elegant way of describing one of the formulae given above.

…but by increasing the complexity of the terms of the series and using factorials, an even better method is possible:

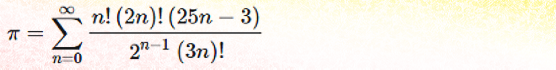
Factorials, for those who don’t know (or don’t remember) are a series of numbers that are multiplied by each other:

So:

• 3! (described as “Factorial three” or “The Factorial of three”)= 3 × 2 × 1 = 6,
• 5! = 5 × 4 × 3 × 2 × 1 = 120, and
• 10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800.

Rolling Non-Repeating Decimal Functions

There used to be a monthly magazine called Science Digest, which I quite enjoyed reading.

In the January 1990 issue, it reported on a mathematical breakthrough by two brothers, Gregory and David Chudnovsky, who extended the calculation of pi to over a billion decimal places using a new algorithm that they had developed for the purpose.

It was the sheer brilliance of how this algorithm worked that really caught my attention, even more than the feat itself. In essence, if you fed it 14 digits of pi, it would spit out the next 14 digits of pi. The formula itself is a fairly ugly thing, but it works.

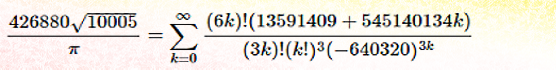
This formula yields digits of pi about 14 at a time. You need to input the previous 14 to get the next ones.

Their work (and that of several subsequent researchers) was actually built upon the brilliance of an Indian mathematician, Srinivasa Ramanujan, who developed a number of innovative formulas for the calculation of pi in 1914.

To me, Ramanujan’s technique is more elegant:

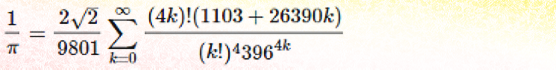
…but there is no arguing with results. It’s entirely likely, however, that without Ramanujan’s formulations, the Chudnovsky brothers would not have been able to make their own breakthrough.

In fact, for technical reasons, the approach used by the Chudnovsky brothers is used for all record attempts these days, and the current record (set on my Birthday this year by Emma Karuka Iwao of Japan, and announced after verification just two months ago) extends the record to an astonishing 100 trillion digits (10^14, or 100,000,000,000,000)

Digit Extraction Algorithms

Astonishingly, this is not the last word on the subject! In 1997, David H Bailey, Peter Borwein, and Simon Plouffe published a paper describing a new formula for π, now known as the BBP formula.

The BBP formula, or others like it, are now used extensively to test digits of pi calculated using the Chudnovsky formula or some variation.

This was capable of extracting any given digit of pi without calculating the preceding digits – in base-16.

You heard me. Base-16, better known as hexadecimal.

Hexadecimal uses A, B, C, D, E, and F to signify the decimal numbers 10, 11, 12, 13, 14, and 15, respectively.

I chose the hexadecimal code pretty much at random, so I was astonished to discover I had selected a named color!

If you were to count to 36 in hexadecimal, it would be “1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21, 22, 23.” Because hexadecimal was often used in computer hardware programming, it is traditional to pad the leading values with “Ø,” signifying zero (and distinguishing it from “O” which could cause all sorts of problems in computer programs if incorrectly substituted for a zero). Each character in hexadecimal occupies one byte in a computer’s memory or disk space.

The range 00-FF in hex is particularly significant, because of the RGB color schema, in which each component in a color is specified by just such a two-byte character. “FF0000” thus specifies Red, “FFFFFF” is white, “000000” is black, and “C4D14A” is named “Americium” but is actually a medium-light yellowish-green in color: Most software these days would use the decimal number from the user’s point-of-view (196, 209, 74) – but rest assured that the number is stored in hex in the computer!

So…. hexadecimal.

This is an example of what is now referred to as a Digit-Extraction Algorithm. Mathworld defines these as an algorithm or expression that “allows digits of a given number to be calculated without requiring the computation of earlier digits.” and adds, “The BBP formula for pi is the best-known such algorithm, but an algorithm also exists for e.”

In 1996, Plouffe derived an algorithm to extract the nth digit of π using base-10 math to derive base-10 digits. It can even be used with a pocket calculator!

The problem is that this calculation is quite slow, in fact several of the earlier calculations offered are faster, notably that devised by the Chudnovsky brothers. Yet, the fact that one base-10 formula has been found, however inefficient, implies that there will be more to be found, so the question of whether or not one can approach the BBP formula in speed remains open..

The Golden Ratio

I was also intrigued to notice, amongst the many formulas listed on the relevant Wolfram Mathworld page, a couple of formulas that referenced the Golden Ratio. This is yet another irrational number, symbolized by the Greek letter phi (φ) and defined as the ratio for which this expression:

…is true.

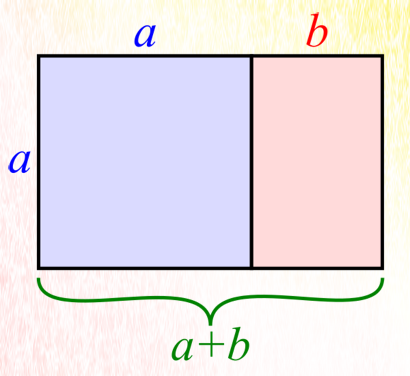
Which sounds really esoteric, an intellectual exercise. Here’s another way to look at it, provided by Wikipedia:

Image by Ahecht (Original); Pbroks13 (Derivative work) – Own work, Public Domain, Link.

This rectangle has one side of length a and another or length a+b. If you cut the long side to create a square of size a × a, you are left with a rectangle of size a × b, with a now the long side, and which has the same exact proportions as the original rectangle. If you calculate the ratios for which the above is true, you get a value of approximately 1.618.

Again, this seems like an interesting bit of trivia, but nothing important.

But the golden ratio keeps showing up in all sorts of unexpected places. Some of them are man-made, and represent ideals of aesthetics that might be self-fulfillment of standards.

• For example, the most popular size of postcards (and postage stamps for that matter) are in the Golden ratio.
• If you calculate the ratio of entries in a Fibonacci sequence* – the next term in a sequence is the sum of the two preceding numbers – the average ratio will be the Golden Ratio.
• Sunflower florets form natural spiral patterns which are said to contain Fibonacci sequences, and which therefore involve the Golden ratio.
• Ditto the arrangement of leaves on a plant stem.

I previously wrote about Fibonacci Sequences in The Meta-Physics of Magic (I thought I had looked at the subject even more extensively, because it’s very useful for RPG design, and usually overlooked, but evidently not – so that’s something I’ll have to do at some future point).

There are others, some confirmed, some disputed.

The last place that I expected one to show up, though, was in a formula to calculate the value of π!

References

Before I get into the concept that I think I intended to broach, I thought that I should list the references that I used in compiling the above information. In no particular order:

• Peter’s answer to “Can pi be expressed by a series” [Quora]
• π Formulas [Wolfram Mathworld]
• Pi [Wikimedia]
• Approximations of π [Wikipedia]
• Chronology of computation of π [Wikipedia]
• 0 (Zero) History [Wikipedia]
• Integer [Wikipedia]
• Infinity Mathematics [Wikipedia]
• Irrational Number [Wikipedia]
• e (mathematical constant) [Wikipedia]
• Circle, Analytic Results [Wikipedia]
• Series that converge to π quickly [Mathematics Stack Exchange]
• #c4d14a- Turmeric Hex Color Code [hexcolor.co]
• Factorial [Wikipedia]
• Digit Extraction Algorithm [Wolfram Mathworld]
• Bailey-Borwein-Plouffe formula [Wikipedia]
• Golden Ratio [Wikipedia]

I think that’s all of them!

Games

In some respects, the increasing complexity of decimals is synonymous with the increasing complexity of RPG plotlines. Well, it’s at least a metaphor, one that’s worth exploring.

The simplest possible plot is something like “PCs see bad guy. Bad guy sees PCs. Bad Guy attacks. Someone wins.” – or, “PCs are hired to deliver a package. PCs deliver package. PCs get paid.”

This is akin to having no decimal places at all, within this analogy.

As soon as you introduce a decimal place, you are introducing a complication. “PCs are hired to deliver a package. Someone attempts to steal the package.” Suddenly, there are two paths for the adventure to take – either the PCs win, and get to deliver the package, or the thieves make off with it and the PCs have to get it back, then deliver it.

A longer decimal is akin to a complication being a gateway to a longer chain of events. “PCs are hired to deliver a fabulous gem. Someone attempts to steal it, but is beaten off. PC discovers that the gem is a fake – is it possible that the real gem was stolen during the earlier attempt, which may have been just a distraction, or was it always a fake? Is their whole mission to be a stalking horse, a lightning rod for trouble while the real gem is smuggled in by some more secret route? Or are they part of a plot to replace the real gem with this fake?

Perhaps there are multiple groups involved, with different intentions and agendas, so that more than one of these speculations is true. Or perhaps the GM decides that whichever plot the PCs choose to investigate third is true. This is akin to a longer repeating decimal string, except that a cap has been placed on the number of times the string will repeat – call it a rounding error! And the ‘true plot’ is positionally significant.

Superficially, several investigative sub-plots like the ones implied by these “theories of the crime” might be similar, but the clever GM will take active measures to differentiate between them. Different tones, different moods, different oppositions with different rules of engagement, settings that are at least somewhat different, NPCs with different personalities.

When the PCs actions have repercussions into the future, such that these investigations are each the beginning of a long road, the campaign (and possibly the adventure) have become recursive, and the role of the GM has changed from that of ringmaster to that of agent provocateur. He is no longer directing the campaign, he is creating a landscape for the players to explore, or not, as they choose.

And, of course, in the long term, the campaign therefore becomes – or should become – more like an irrational number, a series of decimals that never repeats (though at times it might seem to – a decimal string “141592” can occur thousands of times within the length of π for example! The fact that one of those occurrences happens to be at the very beginning of the decimal series of digits is completely irrelevant.

It might seem at first that sandboxing is more akin to the notion of Digit Extraction, in which a given digit is extracted only when it is needed, but I would argue that it more closely resembles the Chudnovsky approach, because the content is inevitably derived from, and dependent on, the “terrain” that has already been explored by the players.

Having at least constructed a basic outline of everything, with embedded plot hooks and (metaphoric) landmines waiting for the PCs to step on them, which can be expanded upon at need, is far more accurately described by the digit extraction analogy; the digits of π don’t change, if you extract the same digit by several different methods they will all give the same answer. You may not know what that digit is when you start, but it’s not like Schrodinger’s Cat, it doesn’t exist in some quasi-metastable state until actually determined.

A Mnemonic Device

Aside from being at least somewhat interesting in its own right, that means that an understanding of decimals makes them a mnemonic device for reminding the GM how to construct plots.

You start with the simplicity of “The PCs are hired to deliver a package. The PCs deliver the package. The PCs get paid,” and build complications and permutations and choices – and yes, a little randomness and chaos – upon that foundation. Where you stop is up to you; this could be the introduction to an entire campaign or it could be the teaser before the title sequence, with the main movie (which may or may not be related in some way to the teaser) still to follow.

Okay, so this won’t get posted on time – as I write this, I still have a lot of formulas and equations to edit and upload, and the text has to be spellchecked and edited, and all those references converted to hyperlinks.

If the graphics were done already, it might just have been possible; without that, it’s not.

So this is being made public a day late. Sorry, everyone; I’ll try to do better next time!